To calculate the Interquartile Range (IQR), we can use either the QUARTILE.INC or PERCENTILE.INC functions in Google Sheets.
The Interquartile Range, the middle 50% of a dataset, is a statistical measure that describes the variability of a dataset.
We can calculate the IQR as the difference between the third quartile (Q3) and the first quartile (Q1) or between the 75th percentile and 25th percentile.
Calculating the Interquartile Range Using the QUARTILE.INC Function
In this example, we will utilize the data in cell range A2:A14 to compute the Interquartile Range in Google Sheets. Here is the syntax of the QUARTILE.INC function in Google Sheets.
Syntax:
QUARTILE.INC(data, quartile_number)In cell range A2:A14, consider the dataset: 6, 11, 12, 15, 22, 40, 45, 60, 62, 63, 65, 66, 70.
Formula:
=QUARTILE.INC(A2:A14, 3)-QUARTILE.INC(A2:A14, 1) // returns 48Where:
QUARTILE.INC(A2:A14, 1)represents the first quartile.QUARTILE.INC(A2:A14, 3)represents the third quartile.
This formula calculates the difference between the third quartile and the first quartile, providing the Interquartile Range (IQR) for the given dataset.
Calculating the Interquartile Range Using the PERCENTILE.INC Function
In this example, we will use the sample dataset from the above illustration to compute the Interquartile Range (IQR) using the PERCENTILE.INC function in Google Sheets.
Syntax:
PERCENTILE.INC(data, percentile)Formula:
=PERCENTILE.INC(A2:A14, 0.75)-PERCENTILE.INC(A2:A14, 0.25) // returns 48Where:
PERCENTILE.INC(A2:A14, 0.25)returns the 25th percentile (first quartile).PERCENTILE.INC(A2:A14, 0.75)returns the 75th percentile (third quartile).
This formula calculates the difference between the 75th percentile and the 25th percentile, providing the Interquartile Range (IQR) for the given dataset.
Calculating Interquartile Range for Multiple Datasets in One Go in Google Sheets
When handling multiple datasets, particularly in data analysis or statistical tasks, the capability to calculate the Interquartile Range (IQR) for all datasets simultaneously can save time and streamline the analysis process. Additionally, it facilitates a straightforward comparison of the spread or variability among each dataset.
To achieve this, you can utilize the BYCOL or BYROW lambda functions along with the aforementioned IQR calculations, depending on the data layout.
If the data is arranged in columns, use the BYCOL function; otherwise, use the BYROW function.
In this example, the data is arranged in columns, specifically in datasets A2:A14 and B2:B14.
Let’s use the QUARTILE.INC function with BYCOL to return the IQR of both datasets in one go.
=BYCOL(A2:B14, LAMBDA(val, QUARTILE.INC(val, 3)-QUARTILE.INC(val, 1)))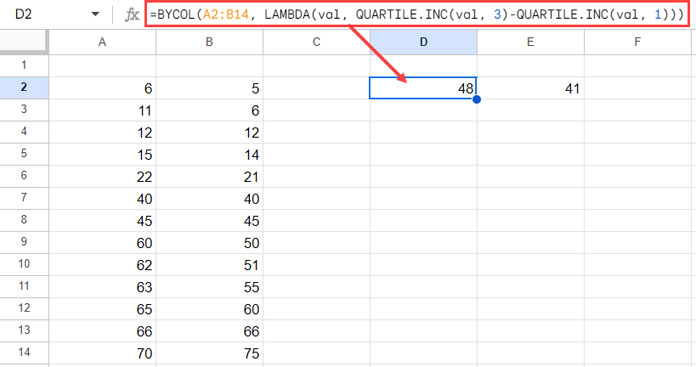
Formula Breakdown:
The formula instructs Google Sheets to iterate over each column in the range A2:B14 (columns A and B) and for each column, it calculates the IQR of all the values in that column. So, it returns two separate IQRs, one for each column.
BYCOL(A2:B14, …): This function processes columns in a specified range, iterating over columns A and B.LAMBDA(val, QUARTILE.INC(val, 3)-QUARTILE.INC(val, 1)): This is a lambda function that defines a small anonymous function to be executed on each value (val). The function calculates the IQR of the elements withinval.
You can replace the function LAMBDA(val, QUARTILE.INC(val, 3)-QUARTILE.INC(val, 1)) with LAMBDA(val, PERCENTILE.INC(val, 0.75)-PERCENTILE.INC(val, 0.25)) as well.
So the formula that calculates the Interquartile Range of multiple datasets using PERCENTILE.INC with BYCOL will be as follows:
=BYCOL(A2:B14, LAMBDA(val, PERCENTILE.INC(val, 0.75)-PERCENTILE.INC(val, 0.25)))Frequently Asked Questions
Here are some FAQs regarding finding the Interquartile Range in Google Sheets.
Questions and Answers:
- Can we use open ranges in the IQR calculation?
- Answer: You can use open ranges such as A2:A or A:A in IQR calculations.
- Do I need to sort the data before quartile or percentile calculations?
- Answer: No, sorting the data is not necessary. The functions will handle the calculations regardless of the data order.













Pretty cool!